Przeliczanie sondaży, przeliczanie głosów

Dodaj komentarz

Jak obliczyć, na ile mandatów może liczyć partia, jeśli znamy tylko ogólnopolskie wyniki sondaży? Są tu dwa podejścia, niczym przysłowiowe dwie szkoły – falenicka i otwocka. Pierwsza próbuje zrobić to tak, jak to się odbędzie, to znaczy obliczać podział mandatów dla każdego z okręgów z osobna. To jednak wymaga przyjęcia jakiegoś wzoru, opisującego jak np. ogólny wzrost poparcia o 1 pp. przekłada się na zmianę w każdym z okręgów. Można założyć, że poparcie wzrasta wszędzie o tyle samo, czyli 1 pp. – lecz może sensowniej byłoby przyjąć, że wzrosty są jakoś zróżnicowane i zależne od stanu wyjściowego. Takie szacunki można poczynić na podstawie wcześniejszych wyników wyborów. Tylko skąd mamy pewność, że kolejne zmiany będą mieć takie same charakterystyki, jak zmiany kilka lat wcześniej? Łatwo tu o błąd. Dlatego sam skłaniam się do drugiej szkoły, która opiera się na odkryciu, jak system D’Hondta przekształca głosy na mandaty (naukowy opis znaleźć można tu). Obrazowy opis tego mechanizmu jest oparty na metaforze kociołka i chochelki – partie przygotowują razem posiłek i każda z nich wrzuca do wspólnego kociołka pół mandatu za każdy okręg. Zawartość kociołka to zatem liczba partii razy 20,5. Potem każda z nich wyjada z kociołka mandaty chochelką wielkości swojego procentowego poparcia. Czyli w przypadku rywalizacji pięciu partii, ta z nich, która ma 40% poparcia dostanie jakieś 40 mandatów – po odliczeniu wcześniej poniesionych „kosztów” będzie mieć zatem „zysk” około 20 mandatów. Taka zaś, która ma 10% poparcia, wyje z kociołka tylko jakieś 10 mandatów, czyli będzie mieć 10 mandatów mniej, bo przecież wcześniej wrzuciła tam swój „wsad do kotła” w postaci 20,5 mandatu.

Takie przeliczenie jest proste – nie wymaga obliczania wyników dla każdego z okręgów z osobna. Prosta tabelka w Excelu pozwala od razu podzielić mandaty między partie. Tylko to zakłada, że wynik nie jest w żaden sposób skrzywiony. Tymczasem są dwa źródła możliwych skrzywień.

Po pierwsze siła głosu w poszczególnych okręgach nie jest równa. Zależy od liczby przydzielonych mandatów oraz różnic we frekwencji. Jeśli więc jakaś partia ma 30% poparcia, to może się okazać, że – jeśli ma większe poparcie w okręgach o niskiej frekwencji – że ono realnie odpowiada jednak np. 31%. Jeśli jednak jej poparcie jest w takich okręgach niższe od średniego, to jej realna siła może spaść do – powiedzmy – 29%.

Po drugie, ogólny wzór zakłada, że żadna partia nie miała szczególnego szczęścia ani wyjątkowego pecha i głosy zmarnowane w każdym z okręgów – naddatki na kolejny mandat, czyli właśnie ten „wsad” wrzucany do kociołka – odpowiadają średnio połowie mandatu. Można to sobie wyobrazić tak, że dla każdego z okręgów rzucamy kostką w grze o wielkość naszej straty. Jeśli rzucimy wyniki 1-3 to tracimy mandat, jeśli 4-6 nie. Powinniśmy stracić średnio 0,5 mandatu na okręg. Taka byłaby logika całego mechanizmu, gdybyśmy mieli nieskończenie wiele okręgów wyborczych. Lecz naszych okręgów jest 41. Nie działa tu jeszcze prawo wielkich liczb, lecz też szczególne odchylenia są bardzo mało prawdopodobne. Jakieś jednak mogą się zdarzyć.

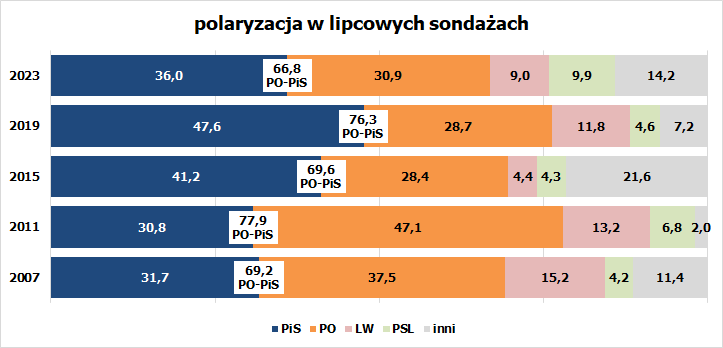
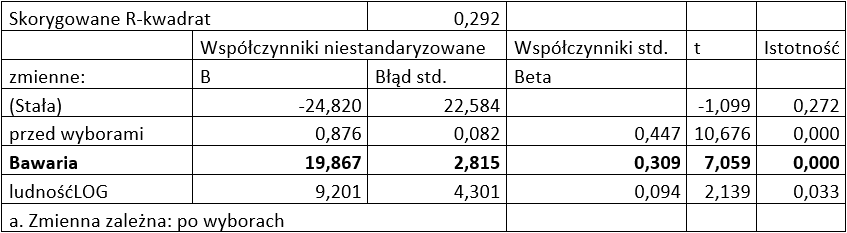
Mam świadomość, że takie odchylenia występują. Przekonują o tym dwa zestawienia. Pierwsze pokazuje, jakie różnice w liczbie zdobytych mandatów wynikały z uwzględnienia różnej siły głosu w okręgach. Policzyłem to tak, że głosy z każdego okręgu zważyłem ogólną siłą głosu, czyli liczbą głosów ważnych przypadającą na jeden mandat. Tak można ustalić efektywny procent poparcia. Taki procent przeliczyłem „chochelką” i odjąłem od wyników te ustalone na podstawie oficjalnych procentów poparcia. Wykres pokazuje takie nadwyżki i straty dla każdej partii czy kategorii partii osobno, lecz także bilans dla trójki partii tworzących dziś „Blok Senacki”. W czterech ostatnich wyborach wyglądało to tak:

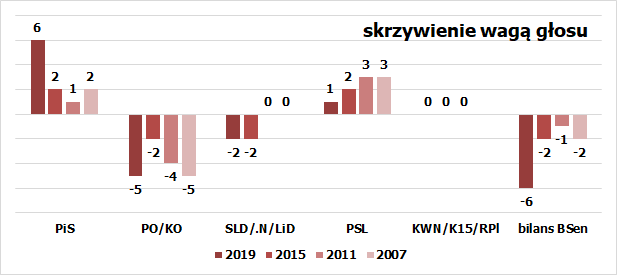
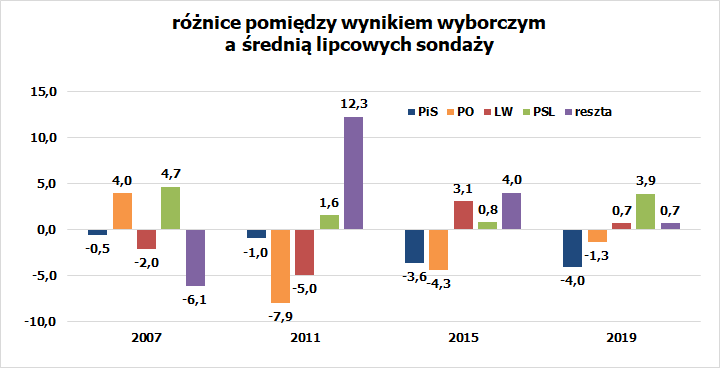
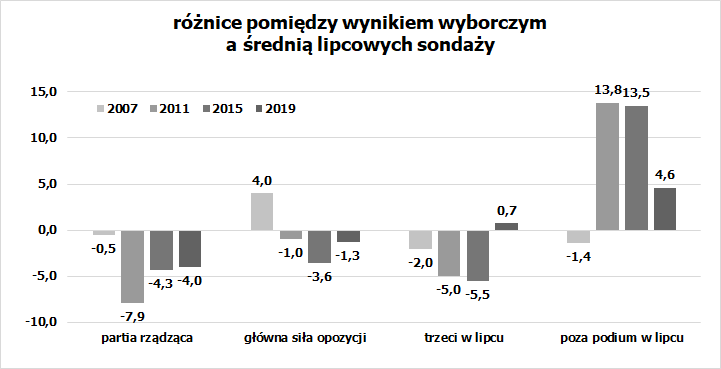
Widać, że są tu pewne wzory odchyleń, lecz przyjęcie na ich podstawie poprawki dla tegorocznych sondaży proste nie jest. Zanim do tego wrócę, jeszcze oszacowanie drugiego rodzaju odchyleń – takich, których nie da się wytłumaczyć systemowymi efektami. To różnica pomiędzy modelem z uwzględnieniem skrzywień wagą głosu a realnymi wynikami. Te wyglądały tak:

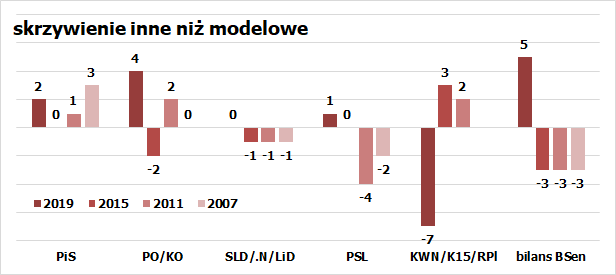
Tu już żywcem nie widać żadnych niepodważalnych wzorów. Każdej z dużych partii choć raz udało się idealnie wpasować w model. Bilans Bloku Senackiego wydawał się przez trzy kadencje stale ujemny, bo w ostatniej przeskoczyć zdecydowanie na drugą stronę. Poparcie dla Palikota i Kukiza układało się szczęśliwie, dając im dodatkowe mandaty, zaś zastępująca ich w roli czarnego konia Konfederacja była największym pechowcem.

Te odchylenia można teraz dodać, pogrupować dla każdych wyborów oddzielnie i na koniec porównać z błędami sondaży – konkretnie zaś z różnicą pomiędzy realnymi wynikami a przeliczeniem „chochelką” średniej sondaży z ostatniego tygodnia (na podstawie zestawienia przygotowanego na potrzeby konkursu „Pytia”).

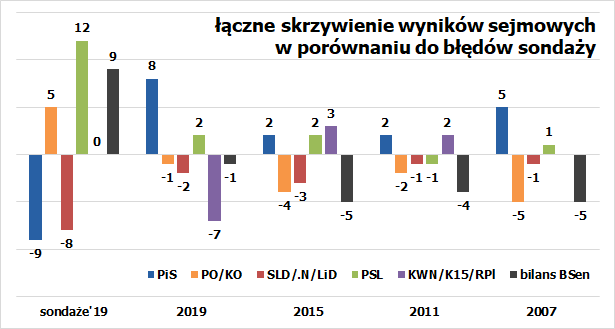
Gdyby ktoś miał na temat skrzywień wynikających z dystrybucji głosów każdej z partii pomiędzy okręgami genialną wiedzę i w ostatnim dniu kampanii, w oparciu o poprawkę z tego wynikającą, przeliczył średnią ostatnich sondaży, to jego prognoza niezwykle rozminęłaby się z rzeczywistością. PiS miałby w takiej prognozie 250 mandatów. Poprawka spotęgowałaby błędy sondaży.

Dodatkowo, model pozwalający przewidzieć odchylenia od standardowych spodziewanych wyników, trzeba nakarmić jakimiś danymi. Mogą to być sondaże (jak widać, o za małej precyzji) albo wyniki wcześniejszych wyborów. Testem trafności modeli stworzonych w oparciu o wcześniejsze dane, jest sprawdzenie, jaki jest błąd oszacowania dla dowolnego przypadku ze zbioru bazowego, jeśli stworzyć model w oparciu o wszystkie pozostałe przypadki. Tu mamy bazę w postaci czterech jedynie wyborów, więc można to sprawdzić dla każdej kombinacji. Czyli dla każdych wyborów z lat 2007-2019 liczymy średnie skrzywienie dla danej partii z pozostałej trójki głosowań i odejmujemy to rzeczywiste. Wychodzi to tak:

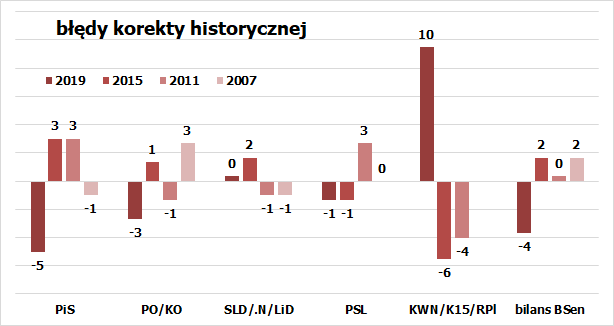
Odchylenia te nie są znacząco mniejsze niż precyzja samej „chochelki”, zastosowanej bez żadnej korekty. Tu akurat uwzględnienie historii choroby nie bardzo pomaga w przewidywaniu, co się nam przytrafi następnym razem. To właśnie dlatego wolę rozwiązanie prostsze, tylko powiązane z kluczowym zastrzeżeniem – to się może potoczyć trochę inaczej, ale nie mamy mocnych podstaw by sądzić, w którą stronę. Mamy po przeliczeniu generalne wyobrażenie, w którą stronę to idzie, lecz szczegóły, to i tak dopiero wyjdą w praniu, w noc powyborczą.

Moje podejście różni się jeszcze pod jednym względem od opinii niektórych zwolenników stosowania poprawek. Nie przychodzi mi do głowy twierdzić, że oni są niekompetentni i nieuchronnie tkwią w błędzie. Oni próbują po swojemu, ja po swojemu. Nie trzymam swojej wiedzy pod korcem – tabelkę w Excelu, pozwalającą w minutę przeliczyć wynik sondażu na mandaty, wysyłam wszystkim chętnym. Przypuszczam, że autorzy bardziej złożonych modeli nie będą chcieli wprowadzić postronnych w tajniki swojego podejścia. Choć może się mylę – w każdym razie chętnie bym się z tym podejściem zapoznał. Może mnie przekonają.

PS. Próbowałem kiedyś namówić kolegów-matematyków na stworzenie modelu rozrzucającego sondażowe poparcie po okręgach. Odpowiedzieli mi, że to się da zrobić tylko naruszając newralgiczne założenia o spodziewanych rozkładach poparcia i frekwencji. Choć zawsze można zastosować jakiś inny rozkład:

Obrazek z bardzo ciekawego opracowania Ireneusza Sadowskiego.

Lipcowe sondaże, lipne prognozy

Dodaj komentarz

Czy lipcowe sondaże to źródło lipnych prognoz? W uzupełnieniu do tekstu w Tygodniku Powszechnym trzy wykresy pokazujące przywołane tam dane.

Najpierw zestawienie średnich lipcowych sondaży z 16 ostatnich lat. Wyróżniono dominujący duet, dwóch mniejszych udziałowców „bandy czworga” oraz pozostałych, pokazanych jako jedna kategoria. Nazwy bez wnikania we wszystkie metamorfozy:

Twierdzenie, że w Polsce pogłębia się polaryzacja to – w świetle tych danych – raczej myślenie życzeniowe. Może to jednak tylko cisza przed burzą? Wykluczyć się tego nie da, lecz jak dotąd zmiany szły częściej w stronę depolaryzacji niż polaryzacji. Na początek porównanie według partii:

Niewielką polaryzację widzieliśmy przed 16 laty. Od tego czasu nasz osławiony „duopl” wychodził z kampanii osłabiony. Osiągnięcie przez PiS „czwórki z przodu” wymagałoby odwrócenia trendu, dość tu jednak widocznego, nawet jeśli to tylko cztery przypadki.

Można to jednak też pogrupować inaczej, uwzględniając pozycję względem władzy i rankingi. Wygląda to wtedy tak:

Generalnie spodziewać się można jeszcze całkiem znaczących zmian, choć lipcowe radości z miejsca na sondażowym podium w pięciu na sześć przypadków przynosiły potem rozczarowanie. Choć z drugiej strony trzeba mieć też na uwadze, że w ostatnich miesiącach sytuacja była całkiem stabilna:

Żadnego tsunami tu na razie nie widać, zaś ewentualne „równie pochyłe” to na razie są takie raczej „płaskawe”. Media są złaknione dramatycznych zwrotów akcji, lecz wygląda na to, że im bardziej ich pragną, tym bardziej ich brakuje. Walka jest wyrównana a słabości wszystkich pięciu stron na razie nie zapowiadają gwałtownych zmian. Pewnie jednak stopniowo rozgorączkowanie będzie mieć głębsze źródła. Do tego przyjdzie wrócić w pierwszych dniach września.

PS. Wyjaśnienia co do metodologii – wszystkie sondaże i wyniki są standaryzowane tak, że pominąłem niezdecydowanych oraz te partie, które ani w lipcowych sondażach, ani w październikowych wyborach, nie przekroczyły 2%.

Obwodowe dogęszczanie

Dodaj komentarz

Wokół nowelizacji kodeksu wyborczego, zmieniającej reguły tworzenia obwodów głosowania, krąży wiele mitów. Zapraszam na opowieść, która pokazuje efekty moich analiz tego problemu. Czy ta zmiana jest potrzebna mieszkańcom Dołów bądź Dziadowej Kłody? Czy może zniechęca ich do głosowania coś innego niż lokalizacja komisji wyborczej?

Cud nad Dnieprem

4 komentarze

Wszystko wskazuje na to, że plan podbicia Ukrainy przez Rosję Putina zupełnie się załamał. Nie ma wątpliwości, że przesądził o tym twardy opór Ukraińców. On sam mógłby jednak nie wystarczyć, gdyby nie coraz powszechniejsze wsparcie zewnętrzne. Lecz ono było właśnie jego kluczowym efektem. Pierwsze komentarze zachodnich polityków – szczególnie niemieckich – miały w sobie stałą nutę defetystycznej bezradności. Wpisywało się to strategię „czterech etapów”, z serialu BBC „Yes, Minister” – w oryginalne przypisywaną brytyjskiemu MSZ, lecz rozsławioną jako recepta Borisa Johnsona na pandemię: na pierwszym etapie mówimy, że nic się nie wydarzy, na drugim – że coś się może wydarzy, lecz nic nie powinniśmy z tym robić, na trzecim, że coś powinniśmy z tym zrobić, lecz nic nie możemy, na czwartym – coś moglibyśmy z tym zrobić, lecz jest już za późno.

Nie jest niczym zaskakującym, że pomaganie skazanej na porażkę ofierze jest bardziej wymagające, niż układanie się z wygrywającym bandytą. To, do czego doprowadził ukraiński opór, nie jest już jednak żadnym dylematem. Każdy woli pomóc wygrywającej ofierze, niż wyrażać zrozumienie dla przegrywającego bandyty. Szczególnie, gdy sytuacja wpisuje się w schemat Dawid-Goliat. Właśnie ta dysproporcja, będąca źródłem wcześniejszego defetyzmu, jest dziś atutem Ukrainy. Żeby teraz odmówić z nią solidarności, trzeba byłoby mieć determinację. Nawet wielu etatowych „usprawiedliwiaczy” w rodzaju Salviniego czuje już, skąd wieje wiatr.

Narastająca z każdym dniem ukraińska pewność siebie stała się kluczowym czynnikiem tej wojny. Widać ją w dzisiejszych nagraniach z walk ulicznych w Charkowie. Rosyjscy żołnierze poruszają się niepewnie i reagują strachliwie. Ukraińcy są zdecydowani i całkiem wyluzowani, jak na sytuację, w której się znaleźli. Tak się zachowuje wygrywająca armia.

Sytuację Rosjan pogarsza oparcie całej tej wojny na jednej koncepcji. Najwyraźniej myśleli, że będzie tak jak w Bagdadzie czy Kabulu – w obliczu ich niepodważalnej militarnej przewagi wszyscy się rozpierzchną lub powitają wiernopoddańczym ukłonem. To, że się tak nie stało, nałożyło się na drugą ważną cechę tej wojny, poza oczywistą dysproporcją sił. Jest nią społeczne podobieństwo stron. Zrozumiały język (a niejednokrotnie po prostu ten sam), brak znaczących różnic religijnych (nie mówiąc już o rasowych), czy wreszcie wspólne doświadczenia i upodobania, wymuszają na agresorze ograniczenie środków. Widać to w scenach zatrzymywania czołgów przez zdesperowanych Ukraińców czy wrzucanych do sieci słownych utarczkach cywili z najeźdźcami. Gdyby ćwierć wieku temu jakiś Czeczen położył się przed rosyjskim czołgiem, ten by pewnie jeszcze przyspieszył. Choć przecież leżący byłby obywatelem tego samego kraju. To, że Putin uwierzył w swoją propagandę dotyczącą Ukrainy, było najwyraźniej przyczyną braku „planu B”. Lecz to, że jego żołnierze wierzą, że Ukraińcy to tylko chwilowo zagubieni bracia-Rosjanie, uniemożliwia stosowanie takich środków, które względem Czeczenów czy Kazachów byłyby pewnie oczywiste – systematycznych powierzchniowych bombardowań i regularnego strzelania do cywili. Stąd zapewne takiego alternatywnego planu nie dało się po prostu stworzyć.

Dziś czas działa na korzyść Ukrainy. Pozostaje pytanie o koszty, jakie musi ona jeszcze ponieść, zanim sytuacja atakujących stanie się tak zła, że będą musieli uciekać z podkulonym ogonem. Atomowe groźby Putina są przerażające – w końcu pięć dni temu nikt sobie nie wyobrażał, że można oblegać kilkumilionową europejską stolicę. Lecz są one najwyraźniej oznaką jego słabości.

Jedno mu się chyba zapewne tylko udało – przejdzie do historii. Tyle tylko, że nie jako ten, który odbudował sowiecko-rosyjskie imperium, tylko ten, który tego upiora przebił osikowym kołkiem. Przecież jeśli Rosji Putina nie udało się przez te cztery dni rzucić Ukrainy na kolana, to znaczy, że jest słabsza niż ktokolwiek sądził. Teraz zaś – poza obnażeniem słabości – dojdzie jeszcze powszechna pogarda dla jej imperialnych ciągot. Mamy za co dziękować Ukraińcom – Слава Україні!

Gang Olsena w amoku

Dodaj komentarz

Jaka piękna katastrofa… Jest już pewne, że wyborów w najbliższą niedzielę nie będzie, choć jeszcze przed tygodniem liderzy PiS zapewniali, że nie ma z tym najmniejszego problemu. Zaś miesiąc temu w ogóle nie rozpatrywali opcji, że coś się może z tym zdarzyć złego. Pytanie jest tylko takie, czy Gowin z najwierniejszymi druhami uratuje im twarz, czy też ją sobie rozkwaszą o ścianę realiów. Gdyby ktoś chciał sobie uświadomić, czym skończy się próba przeprowadzenia wyborów zgodnie z ustawą z 6.04, dziś trochę danych.

Samo korespondencyjne oddawanie głosów wydaje się bezpieczniejsze, bo skraca czas, w którym może dojść do kontaktów głosujących z postronnymi osobami. Dzieje się tak dlatego, że zostaje z głosujących zdjęty obowiązek uczestniczenia w procesie weryfikacji tożsamości po wejściu do lokalu wyborczego. Ma to jednak miejsce tylko wtedy, jeśli obowiązek ten nie zostaje przerzucony na moment kontaktu z listonoszem – w postaci legitymowania się związanego z obowiązkiem dostarczonego pakietu wyborczego do rąk własnych adresata. Jeśli obowiązku legitymowania nie ma, rodzą się spektakularne problemy polityczne – o tym dalej. Lecz nawet taka szalona ekstrawagancja nie likwiduje wszystkich problemów logistyczno-epidemicznych.

W każdym bowiem wypadku wybory korespondencyjne wydłużają czas, jaki administracja wyborcza musi poświęcić na zliczanie głosów. Jej obowiązkiem pozostanie dalej weryfikacja tożsamości głosującego, tylko już bez jego aktywnego udziału. Ten udział miał dotąd formę podejścia do jednego z ponad 100 tys. stanowisk do wydawania kart wyborczych, które są tworzone w obwodowych komisjach wyborczych przy okazji standardowych wyborów. Pod nieobecność obywatela, sprawdzanie tożsamości wymaga wyszukania go w bazie danych na podstawie numeru PESEL. Wymaga też dodatkowych sposobów kontroli uczciwości tego procesu, co z kolei wymaga zaangażowania dodatkowych ludzi i tym samym zwiększa liczbę kontaktów międzyludzkich i czas takich spotkań. Poniższy wykres pokazuje, ile zajmie ustalenie wyników I tury wyborów, gdyby osoby, przewidziane do tego zadania przez ustawę z 6.04, pracowały z taką wydajnością, jak monachijska administracja wyborcza. Po wyborach 29.03 w Monachium 250 sześcioosobowych zespołów przeliczało głosy 560 tys. wyborców przez 18 godzin, co oznacza przeliczenie 1000 głosów w trakcie ośmiu godzin pracy takiego zespołu.

Obliczony na powyższym wykresie czas pracy komisji grozi nieprzeprowadzeniem drugiej tury wyborów w konstytucyjnym terminie (14 dni). Rodzi wątpliwości, czy możliwe jest wykonywanie takiego zadania przez osoby pobierające dietę odpowiadającą zwykle nie więcej niż 20 godzinom pracy. Ustawa z 6.04 daje możliwość poszerzenia składu komisji w nadzwyczajnych okolicznościach. Gdyby takie komisje miały zakończyć swoją pracę w 18 godzin, tak jak to miało miejsce w Monachium, liczba osób, o które trzeba byłoby je poszerzyć, wielokrotnie przekraczałby ich przewidywany ustawą skład. Pokazuje to poniższy wykres.

Tak poszerzone komisje w największych miastach liczyłyby setki członków, co wymaga wcześniejszego wypracowania jakichś szczegółowych procedur i powołania struktur w obrębie komisji. To niezwykle trudne zadanie w krótkim czasie oraz w warunkach epidemii. Do tego w świetle obowiązującego kodeksu wyborczego podział komisji na zespoły jest sprzeczny z prawem. Budzi też poważne zastrzeżenia co do uczciwości wyborów. Nic nie wskazuje na to, by rozważane były obecnie jakieś zabezpieczenia przed tworzeniem zespołów jednolitych pod kątem sympatii politycznych. Rozstrzygnięcia takiego zespołu w sprawie niekompletności pakietu wyborczego są niepodważalne i nieweryfikowalne post factum.

Nie zawracając sobie głowy możliwą logistyczną katastrofą, obóz władzy prze do korespondencyjnych wyborów w nadziei, że ograniczona frekwencja przyniesie mu łatwe zwycięstwo, które wszyscy jakoś w końcu uznają. Oba te przypuszczenia są obarczone ogromnym ryzykiem.

Kluczowym elementem uchwalonego rozwiązania jest dostarczenie pakietów wyborczych wszystkim uprawnionym do głosowania, dodatkowo w postaci druku bezadresowego. Już samo dostarczenie wszystkim takich pakietów może spowodować nieprzewidywalne zmiany zachowań wyborczych. Pokazuje to wykres, na którym przedstawiono liczby głosów oddawanych w II turze wyborów burmistrzów w bawarskich miastach. We wszystkich miastach, niezależnie od wielkości, w wyborach 2020 roku oddano o prawie jedną czwartą głosów więcej niż w poprzednich takich wyborach w roku 2014.

Nie jest wcale oczywiste, czy oznacza to rzeczywisty wzrost obywatelskiego zaangażowania. Zapewne nie ma powodów, by wykluczać taką hipotezę – w wielu wypadkach może to być ułatwienie dla wyborców. Warto jednak rozważyć także inne możliwe hipotezy:

  • Oddawanie głosów za domowników, generalnie niezainteresowanych polityką i wcześniej niegłosujących.
  • Głosowanie za osoby zameldowane pod danym adresem, przebywające poza miejscem zamieszkania.
  • Przekazywanie pakietów sąsiadom, rodzinie, bądź innym osobom znanym osobiście a bardziej zainteresowanym polityką.
  • Aktywne pozyskiwanie przez politycznie aktywnych obywateli pakietów wyborczych od osób biernych politycznie, uzasadniane deklaracjami o pomocy w oddawaniu głosu.
  • Zwiększoną presję społeczną środowisk lokalnych i zawodowych – pozytywna odpowiedź na akcję typu „Go-To-Vote” jest znacznie łatwiejsza w przypadku powszechnego głosowania korespondencyjnego. 
  • Wykorzystanie porzuconych pakietów wyborczych celem zwielokrotnienia siły swojego głosu.

Wszystkie takie działania są szczególnie łatwe w przypadku rozwiązań przyjętych w ustawie z 6.04. Pakiety jako druki bezadresowe nie są zabezpieczone przed przywłaszczeniem – czy to celowym, czy przypadkowym. Jedynym przewidzianym sposobem weryfikacji tożsamości głosującego jest podanie numeru PESEL – tymczasem numer taki jest powszechnie dostępny w internetowych księgach wieczystych. Zdobycie takich numerów wszystkich współlokatorów-współwłaścicieli wymaga kilkuminutowych zabiegów. Kompletnymi spisami wyborców, wraz z ich numerami PESEL dysponują władze lokalne. W odróżnieniu od tradycyjnych kart do głosowania, pakiety nie zasobem o ściśle limitowanym dostępie. Otwiera to drogę do „wyścigu zbrojeń” na polu oszustw wyborczych. W szczególności warto zwrócić uwagę, że istotnym samousprawiedliwieniem dla takich działań jest poczucie krzywdy i bycie stroną w rywalizacji prowadzonej przeciw siłom politycznym oskarżanym o nadużywanie władzy.

Znaczenie takich zachowań w realiach polskich wyborów uzmysławia kolejny wykres. Pokazano na nim uczestników obu tur głosowania w wyborach prezydenckich 2015 – z uwzględnieniem tych, którzy nie brali udziału w głosowaniu, choć byli do tego uprawnieni. Wynik Andrzeja Dudy w II turze rozbito w ten sposób, by pokazać jego przewagę nad Bronisławem Komorowskim – margines zwycięstwa.

Dodatkowe dwa miliony wyborców zdecydowało się wziąć udział w wyborach w ciągu dwóch tygodni dzielących pierwszą turę od drugiej. Była to liczba czterokrotnie większa od marginesu zwycięstwa. Zjawisko takie nie występowało w wyborach prezydenckich 2010 roku. To pokazuje jak nieprzewidywalne są zachowania wyborców.

Jeszcze ważniejsze jest uzmysłowienie sobie, że 13,7 mln wyborców, którzy nie głosowali w 2015 roku, w warunkach ustawy z 6.04 otrzymałoby do skrzynek pakiety wyborcze. Jeden na dwadzieścia sześć z tych głosów wystarczyłby, żeby zmienić zwycięzcę tamtych wyborów. Powstaje pytanie, co stanie się z tymi milionami głosów. I czy ktokolwiek pogodzi się z wynikiem rywalizacji prowadzonej w tak nieprzewidywalnych warunkach? Niezależnie kto wygra, znajdzie on dziesiątki uzasadnień podważających formalny wynik. Nie da się ukryć, że wiele z tych uzasadnień może być przekonujących.

Źle zaplanowane wybory wcale nie muszą zamknąć okres szczególnego politycznego wzmożenia, jakim jest kampania wyborcza. Mogą podnieść takie wzmożenie na znacznie wyższy poziom. Emocje, towarzyszące porażce w rywalizacji są zawsze mniejsze od tych, które są wywoływane przez poczucie i niesprawiedliwości wywoływane przez złamanie obowiązujących reguł.

Są to fragmenty opracowania, do którego link umieszczono poniżej. Samo opracowanie jest pochodną zeszłotygodniowego seminarium Centrum Badań Ilościowych nad Polityką UJ. Samo seminarium też jest nagrane i można je sobie oglądnąć klikając w kolejny link.

Problemy głosowania korespondencyjnego – opracowanie pisemne

Nagranie z seminarium

Ta seria ma już wiele odsłon. Kto nie wierzy, może sprawdzić w linku poniżej. Obrazek spod tego właśnie linka. Kolejny odcinek, po „Gangu Olsena w amoku”, miał tytuł „Ostatni skok Gangu Olsena”…

https://krytykapolityczna.pl/kraj/pis-ordynacja-wyborcza-flis/

Wuhańska katastrofa, wyborcza ruletka

2 komentarze

To, że PiS przeprosił się z głosowaniem korespondencyjnym, które upchał do pakietu antykryzysowego, okazało się mało znaczącą zmianą w ich myśleniu. Dzisiejsze przecieki z partii rządzącej zwiastują chęć dokonania kopernikańskiego przewrotu w organizacji polskich wyborów. Przewrotu zapoczątkowanego w Bawarii, radzącej sobie z problemem niedokończonych wyborów lokalnych. Chodzi o bezkontaktowe rozesłanie wszystkim obywatelom pakietów wyborczych a potem możliwość ich – także bezkontaktowego – odesłania administracji wyborczej. To rozwiązanie anulujące trochę roztrząsanych ostatnio problemów, lecz dodające nowe. Naprawdę ciężkiej wagi.

Znika problem udostępniania szkół i przepustowości urzędów pocztowych, awizowania i odbierania listów poleconych. Lecz problemy logistyczne się mnożą. Urząd miasta Krakowa będzie musiał rozesłać 600 tys. pakietów. Nie wydaje się, by mając na przygotowanie dwa tygodnie, dało się to zautomatyzować. Będzie potrzebna do tego rzesza ludzi. Potem jakieś 450 tys. pakietów trzeba będzie otworzyć i policzyć. W ostatnich wyborach głosy w Krakowie liczyło 4000 osób. Czy do otwierania pakietów i sprawdzania ich zawartości potrzeba będzie więcej osób, czy mniej? Nie sądzę, by ktoś znał odpowiedź. Można dopytać w Bawarii. Tak czy owak, potrzebne będą na pewno zgromadzenia łamiące wszystkie obowiązujące obostrzenia. Mogące przyczynić się do rozprzestrzenienia koronawirusa i podatne na sparaliżowanie, jeśli do zakażenia ich członków dojdzie wcześniej.

Najważniejsza jednak jest inna innowacja – te 150 tys. pakietów, które zostaną gdzieś w narodzie, bo zostaną wysłane do tych, którzy zwykle w wyborach nie głosują. Może jakaś część z nich się skusi i skorzysta z nowej możliwości. Może jednak jakaś część skusi się na coś zupełnie innego. Ciekawe, po ile będzie chodzić taki pakiet na Allegro… Czy będzie przestępstwem obejście sąsiadów i zadeklarowanie pomocy w oddaniu głosu? Czy dopuszczalne będzie podrzucenie koperty do skrzynki, czy może także wyręczenie w postawieniu krzyżyka na karcie? Czy można komuś oddać swój pakiet wraz z podpisanym oświadczeniem, że się głos oddało osobiście? Czy ktoś będzie ścigał takie procedery? Czy sądy będą rozpatrywać protesty wyborcze, poparte nagraniami z kupowania głosów? W 2011 roku Sąd Okręgowy w Świdnicy nakazał powtórzenie wyborów prezydenta Wałbrzycha po ujawnieniu takiej afery. Czy to się teraz może powtórzyć?

Żeby nie być gołosłownym, jedno zobrazowanie problemów, które już pojawiły się w poprzedniej notce. Wykres pokazuje losy pakietów, które zostały wysłane zainteresowanym wyborcom w 2015 roku, gdy każdy mógł, lecz nie musiał, skorzystać z takiej opcji. Zsumowano wszystkie przypadki uznania nadesłanego głosu za niekompletny (czyli niekwalifikujący się do wrzucenia do urny) w jedną kategorię. Głosy, które trafiły do urny podzielono na ważne i nieważne w takiej proporcji, w jakiej dzielił się ogół oddanych głosów. To tylko po to, żeby zobaczyć ogół zmarnowanych pakietów na tle „tradycyjnych” nieważnych głosów.

Udział pakietów, które poszły „na rozkurz”, wielokrotnie przewyższa spodziewaną różnicę pomiędzy kandydatami w ewentualnej drugiej turze. Ciekawe czyi wyborcy będą unieważniać swoje głosy częściej, mając kłopoty z ogarnięciem całej procedury…

W obliczu wuhańskiej katastrofy, obóz rządzący chciałby nam zafundować zabawę w wyborczą ruletkę. Jest bardzo prawdopodobne, że wszystko się posypie od strony logistycznej, nawet po zastosowaniu zupełnie nieortodoksyjnych rozwiązań. Gdyby nawet to jakimś cudem udało się ogarnąć, jest też szansa, że kolosalne zaufanie społeczne, które jest potrzebne do takiego bezkontaktowego głosowania, zostanie przez nadgorliwców nadużyte. Nieomal pewne jest, że przegrana strona, ktokolwiek by nią nie był, będzie miała poczucie kolosalnej krzywdy i będzie obwiniać za porażkę nie swoje słabości, lecz słabości takiej procedury. W tym bębenku jest za dużo kul, by nawet największy hazardzista uznał tę grę za wartą świeczki.

PS. Sprawdziłem sobie jeszcze, że w drugiej turze wyborów prezydenckich 2015, głosowanie korespondencyjne było ponad dwukrotnie popularniejsze w tej części kraju, gdzie wygrywał Komorowski. Z której strony tego nie oglądać, to się całe pruje. Możliwe jednak, że pomysł z powszechnym głosowaniem korespondencyjnym jest potrzebny tylko po to, żeby najwierniejsi i najbardziej zawzięci dziennikarze obozu rządowego mogli jakoś przejść do porządku dziennego nad odwołaniem wyborów – „prezes miał genialny plan, tylko ta podła, kłótliwa opozycja zablokowała to, na co z utęsknieniem czekały miliony Polaków – nie było więc wyjścia, jak wprowadzić stan nadzwyczajny, żeby jakoś ukrócić jej niecne knowania „.

Tragifarsa wyborcza

Dodaj komentarz

Nowe inicjatywy i wypowiedzi obozu władzy w sprawie wyborów wpisują się dobrze w dzisiejszą datę. Tylko nie wiadomo, czy się śmiać, czy płakać. Gdyby ktoś z obserwatorów chciał sobie wyrobić jakieś wyobrażenie o realnych problemach, na które mogą trafić najnowsze pomysły Nowogrodzkiej na przezwyciężenie wyborczych przeciwności, garść faktów.

Zacznijmy od głosowania korespondencyjnego. Dane z dwóch ostatnich wyborów sejmowych (gdzie frekwencja i struktura głosujących jest najbliższa do tej z wyborów prezydenckich) podaje tabela.

Głosowanie korespondencyjne nie wystawiało dotąd ani administracji, ani poczty, na szczególne wyzwanie –  czy to to dostępne tylko niektórym, jak w 2019 roku, czy to dla wszystkich cztery lata wcześniej. Największa liczba kopert, która przyszła do jednej komisji w 2015 roku, to 75. W żadnej gminie nie było do wysłania, ani do późniejszego rozdzielenia pomiędzy komisje, więcej niż 500 kopert. Nikt zatem nie jest przećwiczony w obsłudze masowego wydarzenia tego typu. Tymczasem ono samo w sobie niezwykle komplikuje całą procedurę głosowania. Czyli wymaga do obsługi większych zasobów, w szczególności ludzkich. Dla ścisłości. Zwykłe wybory obsługuje prawie 25000 komisji, w których pracuje 250000 osób. W zwykłej powszechnej komisji głosuje około 1000 osób. W Polsce jest obecnie 7500 urzędów pocztowych, zaś cała poczta zatrudnia około 80000 osób. Do komisji się idzie raz, zaś głosowanie korespondencyjnie wymaga dwukrotnego kontaktu z operatorem procesu – ktokolwiek by nim nie był. Pakietu nie można przekazać obywatelowi bez potwierdzenia, ani nie można bez potwierdzenia odebrać. Pominięcie takiej procedury grozi podważeniem jakiejkolwiek wiarygodności wyborów. Odebranie i nadanie listu poleconego zajmuje z reguły więcej czasu – w szczególności po stronie obsługi – niż wydanie karty do głosowania w komisji. Zmiany, jakie zaszły w naszym życiu, każą przypuszczać, że chętnych na głosowanie korespondencyjnie będą teraz setki tysięcy, jeśli nie miliony. W przeprowadzonych na początku epidemii bawarskich wyborach lokalnych ponad dwie trzecie głosów zostało oddanych w ten sposób. Wprowadzone ustawą, która już weszła w życie, głosowanie korespondencyjne dla osób 60+ byłoby kolosalnym wyzwaniem organizacyjnym i politycznym, nawet gdyby wybory miały się odbyć jesienią. W powyższej tabeli można też zobaczyć, jak dużym kłopotem dla obywateli jest taka nowa procedura – przy umasowieniu głosowania korespondencyjnego liczba pomyłkowych głosów nieważnych może iść w setki tysięcy. Uniknięcie tego wymaga zaabsorbowania ich uwagi, która teraz jest jednak skierowana w zupełnie inną stronę.

Drugim wątkiem jest bunt głównych organizatorów – administracji gminnej. Marszałek Ryszard Terlecki pogroził za to „buńczucznym” samorządowcom komisarzem. Jak już nieraz w jego przypadku, trudno uniknąć wrażania, że powiedział to, co myśli, nie zaś przemyślał to, co mówi. Szybki rzut oka do ustawy i kilkuminutowa konsultacja z prawnikami pozwala ustalić, że taka groźba nie jest zbytnio wiarygodna, na pewno zaś nie ma daje żadnego bezpośredniego wpływu na przygotowania do majowych wyborów. Wprowadzenie komisarza do gminy to całkiem dokładnie opisana procedura, zajmująca minimum 30 dni, za to bez gwarancji powodzenia. Jest zaskarżalna sądownie i wymaga wcześniejszego wezwania do zaprzestania łamania prawa. Nie jestem przekonany, czy nawet osobista interwencja Zbigniewa Ziobry pozwoli znaleźć sędziego, który za coś takiego uzna wysłanie do przewodniczącego PKW pisma informującego o braku możliwości przeprowadzenia wyborów ze względu na sytuację epidemiologiczną. Zaś takich sędziów już teraz trzeba byłoby znaleźć setkę.

Jednak nawet gdyby w ramach próby samorządowego „impeachmentu” jakiś komisarz został przez wójta wpuszczony do urzędu przed wyborami, to trudno sobie wyobrazić, by był w stanie zorganizować głosowanie przy choćby minimalnym biernym oporze pracowników. Dla nich zaś to nie będzie sprawa polityki, tylko zdrowia. W setkach polskich gmin obsługa wyborów po stronie urzędu oznacza nieuchronny bliski kontakt z kilkudziesięcioma obcymi osobami – trzeba wszak fizycznie odebrać od nich protokoły, wcześniej zaś wydać karty do głosowania, pieczątki etc. Wygląda na to, że na Nowogrodzkiej nie ma akurat nikogo, kto widział organizację wyborów z bliska i ma świadomość jak skomplikowane jest to przedsięwzięcie.

Wszyscy ci, którzy w administracji opierają się majowym wyborom, czują za plecami poparcie zdecydowanej większości społeczeństwa. Pokazujące masowy sprzeciw sondaże publikowane są dzień za dniem. Czytają je też policjanci, urzędnicy wojewody, sędziowie i wszyscy ci, których partia rządząca – według krążących przecieków – chciałaby użyć do przywołania do porządku lub zastąpienia lawinowo narastającego grona protestujących. Pójście na zwarcie musi się skończyć jakąś niewiarygodną kompromitacją.

Minęło raptem 10 dni od wywiadu Jarosława Kaczyńskiego w RMF, który ukierunkował działania Nowogrodzkiej. Od tego czasu ściana realiów przybliża się nieubłaganie, lecz szarża wiernej drużyny tylko się rozpędza. Czy jeśli zamknie się oczy, uderzenie o taką ścianę będzie mniej bolesne? Śmiem wątpić.

Wirus i bawarskie wybory

9 komentarzy

15 marca w Bawarii odbyły się wybory lokalne. Do tego dnia w Niemczech zgłoszono 7046 przypadków zakażenia koronawirusem. Z nich 1139 przypadło na Bawarię. W ciągu kolejnych 10 dni w Bawarii przybyło 6851 przypadków, zaś w reszcie kraju 22574. W przeliczeniu na 100 tys. mieszkańców zmiany te wyglądają tak:

W ciągu 10 dni w Bawarii przybyło o 20 przypadków więcej niż w reszcie kraju. W tym czasie w Nadrenii-Palatynacie, gdzie poziom  zachorowań 15 marca był nawet minimalnie wyższy niż w Bawarii, nowych chorych było nieco poniżej 35 na 100 tys. Bawaria jest tu ewidentnym ewenementem.

Powszechnie wiadomo, jakie ryzyko niesie uśrednianie zróżnicowanych przypadków. Dlatego takie ogólne porównanie zostało pogłębione przez analizę na poziomie powiatów. Jej wyniki pokazuje kolejny wykres. Z analizy wyłączono dwa ekstrema – powiat Hainsberg w Nadrenii Północnej, gdzie 15 marca liczba chorych przewyższała pięciokrotnie następny w kolejności przypadek, oraz miasto-powiat Kaufbeuren w Bawarii, gdzie do 25 marca nie zgłoszono żadnego przypadku. Bawarskie powiaty wyróżniono na czerwono. Dla obu grup wykres pokazano najprostszą linię trendu i równanie regresji.


Gdyby ktoś miał wątpliwości, co taki wykres oznacza, to najprościej ująć to można tak – jeśli porównamy dwa powiaty, w których 15 marca była taka sama liczba zachorowań, to 10 dni później w Bawarii było o 17 przypadków na sto tysięcy mieszkańców więcej. Z ogólnej różnicy 20 przypadków, 3 wynikać mogą z początkowego zróżnicowania. Pozostałe zaś mogą oczywiście wynikać z wielu różnych czynników, którymi Bawaria różni się od Nadrenii czy innych części Niemiec. Lecz fakt wyjątkowego masowego wydarzenia, jakim jest powszechne głosowanie i wielogodzinne zbiorowe ustalanie wyników przez komisje wyborcze, wydaje się wyjaśnieniem wysoce prawdopodobnym. Jeśli taka hipoteza jest prawdziwa, to przeprowadzenie wyborów w Bawarii doprowadziło do zakażenia się kororawirusem przez około 2000 osób.

Uwzględniając różnice w wielkości kraju, w przypadku Polski wybory takie jak bawarskie odpowiadałoby za około 6000 nowych zachorowań. Lecz oczywiście są tacy, którzy uważają, że w Polsce nie dzieje się nic, co uzasadniałoby przesunięcie wyborów. W Bawarii też tak na pewno myślano.

Liczba zachorowań na podstawie danych Instytutu Roberta Kocha. Gorące podziękowania za pomoc w ich zdobyciu dla dr hab. Kamila Marcinkiewicza z Uniwersytetu w Hamburgu.

PS. Gdyby ktoś był ciekaw, jak wygląda nieco porządniejszy model, to jego parametry wyglądają tak: